嘿朋友~记得先点蓝字关注我哦~
简介
单质点体系振动是最为简单的振动,通常在学习结构动力学中也是最开始学习这部分的知识和内容,这部分内容最为基础,也非常重要。它包括单自由度体系振动分析中涉及的物理量和基本概念,而且实际运动中,许多的问题也可按单自由度体系计算,比如普通的隔震结构、多自由度在正则化坐标系下的各个自由度均为解耦的单自由度体系。单质点的动力特性在隔震设计中起到指导性的作用,因此获取可靠准确的单质点结构分析结果十分重要,工程中最常用的3款软件为SAP2000、OpenSees、ANSYS,文章在对理论介绍后介绍了三种软件建模过程,起到对结构动力学学习的参考作用。
理论分析:
当结构为单质点自由振动体系时候,通过达朗贝尔原理或拉格朗日方程均可列得到下式:
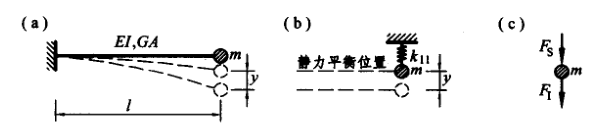
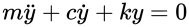
如果设
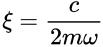
可得到
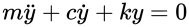
补充:在隔震结构中,若上部结构和含隔震层时的结构周期差别较大时,上部结构可当成一个刚体,可视为单质点的剪切型模型分析。假设一个2自由度(带隔震层的结构和纯上部结构)隔震结构的等效地震反应分析。
隔震结构的周期:
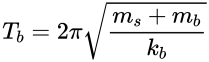
上部结构的周期
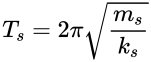
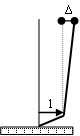
图中△为:
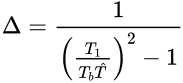
当周期比值
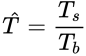
很小的时候,上部结构可以近似为一个刚体,即为单自由度模型,具体的下回再具体解说。
接下来讲解下四种方法:杜哈梅积分(分段解析法)、纽马克β法、威尔逊θ法、Hilber-Hughes-Taylor a(HHT)方法。
01
杜哈梅积分:
在实际工程中,很多动力荷载不是简谐荷载,也不是周期荷载,而是随时间任意变化的荷载,此时可采用的计算方法是杜哈梅积分法。强迫运动方程是线性的,可以运用叠加原理。体系在随时间任意变化的动力荷载作用下的响应,可视作一系列独立瞬时冲量连续作用下响应的总和。因此,只需对瞬时冲量作用引起的微分响应进行积分,便可得到一般动力荷载作用下的响应。如下图所示:
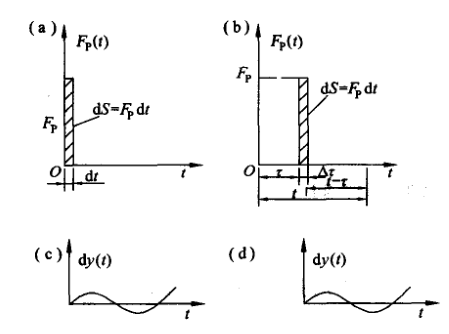
通过冲量可以得到该式子:
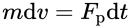
即:
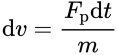
式中,dv为瞬时冲量引起的速度增量。此时质体的位移增量可由上式积分求得,它是时间的二阶微量,可以略去。因此,瞬时冲量作用所引起的微分响应dy(t)即为以dv为初始速度的微幅自由振动,可得:
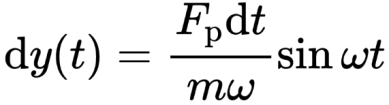
如果冲量是在t=x时作用在体系上的。则在冲量结束以后的任一时刻,则位移表达式为:
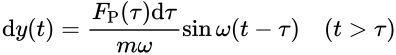
于是,在任意荷载下的位移有:
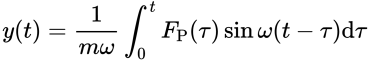
当考虑阻尼影响时,杜哈梅积分位移计算式为:
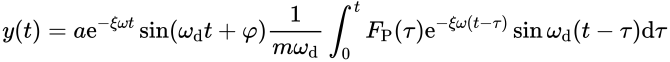
进而,通过数值解法,如梯形公式、辛普森公式等,即可求解上述方程,可得到结果,也可通过对荷载进行分段求解分段解析解组合而成,即为分段解析法。
02
纽马克β法:
为了方便大家理解,小编此处仅罗列纽马克β法的步骤,详情可以翻阅《结构动力学》
(1)初始计算
①组成该体系的刚度矩阵[K]、质量矩阵[M]和阻尼矩阵[C]。
②选择时间步长Δt和积分参数r、β;(为了稳定收敛,通常取r=1/2,β=1/4)
③计算积分常数
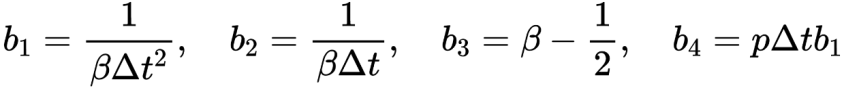
④形成有效刚度矩阵
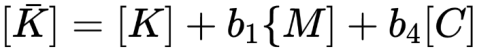
⑤对上矩阵进行三角分解

⑥指定初始条件:

(2)对每一时间步长
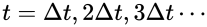
① 计算时刻t+At的有效荷载1
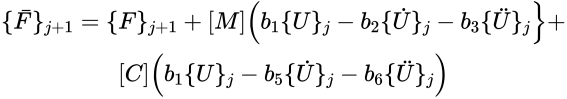
②求解t+Δt的位移
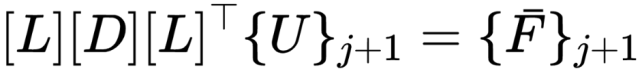
③计算t+Δt的速度和加速度
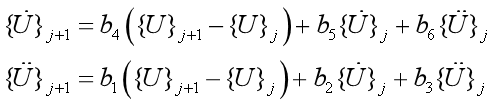
转步骤(2)的①,t=t+Δt,迭代循环,即可求得结果。
03
威尔逊θ法:
Wilson-θ法是常规的Newmark方法通过引入一个系数θ达到了无条件的稳定系数的提出是因为观察到一种现象,即不稳定的解趋向于在真实解附近振荡。因此,如果在时间增量内计算数值解,为使这种振荡减到最小,可以通过如下定义的时间步及荷载对Newmark方法作简单的修改来完成,即
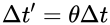
(其中θ>=1.0)
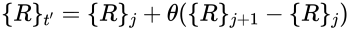
对于Newmark方法进行修正后可得到下式子:
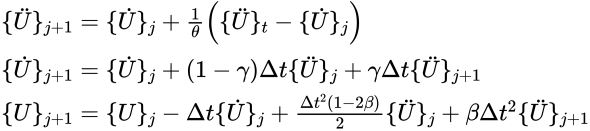
θ系数的使用有助于在体系的高阶振型中去除数值阻尼。如果θ等于1.0,就是Newmark方法。然而,对于高阶振型响应是很重要的问题,引入的误差可能比较大。除此之外,还不能在时间t处精度满足动力平衡方程。因此,若是存在高阶阵型的问题,则不再推荐使用系数θ。
04
Hilber-Hughes-Taylor a(HHT)方法:
a方法使用Newmark方法求解下列修正的运动方程:
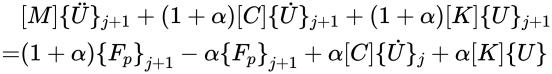
其中a的取值参考范围在0~1/13。
当a等于零时,此方法还原为常量加速度方法。它在高阶振型中产生数值能量损耗。然而,它不能像用刚度比例阻尼那样的阻尼比对其进行预测。同时,它也不能在时间处求解基本平衡方程。然而,当前许多计算机程序都在使用它。该方法的效果似乎与使用刚度比例阻尼法的效果很相近。建议使用默认的HHT方法,除非对其他方法有特定的需要。.在非线性分析中,经常需要使用一个a负值来确保结果的收敏性a。
【例题】为了对比各软件与理论计算结果的误差和展示建模过程,以一个简单的单质点体系作为算例,地震波选取三条人工波,单质点体系的自振周期为2.7s,阻尼比为0.05,提取质点的加速度及位移时程进行对比。
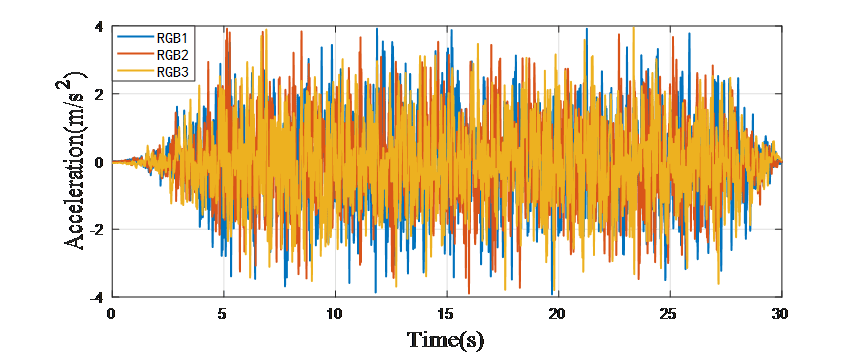
地震波时程

地震波反应谱
(为了对比简洁以下结果仅呈现RGB1的计算结果)
01
SAP2000
Sap2000模型参数设置:

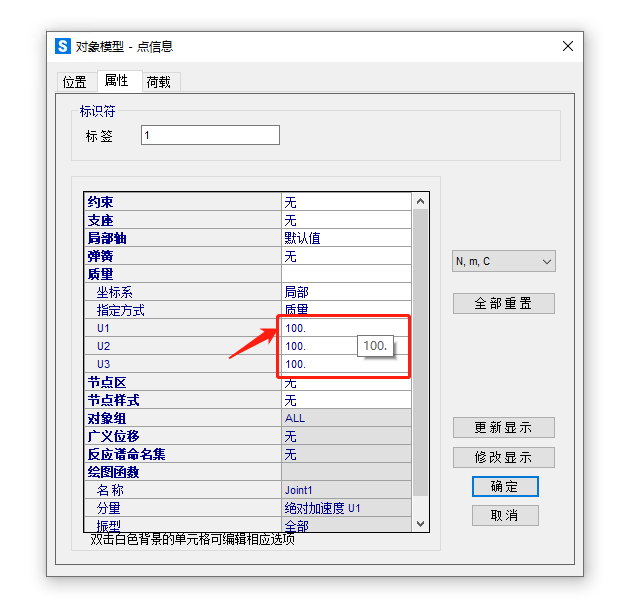


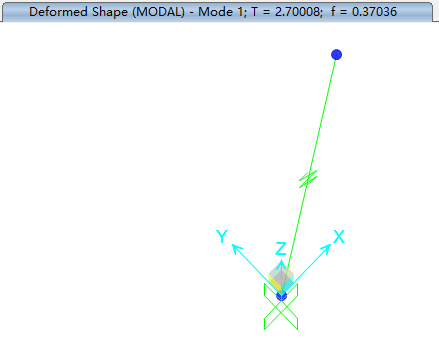
SAP四种求解方法结果对比:

SAP2000加速度时程结果
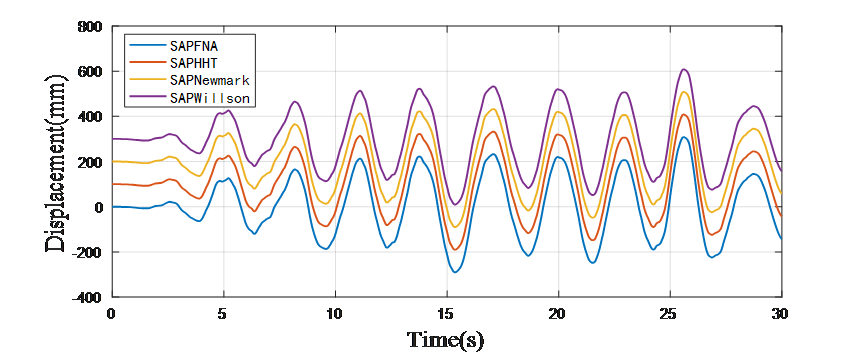
SAP2000位移时程结果
02
ANSYS
ANSYS单质点模型
ANSYS命令流:
/prep7!设置单位为N/m/kg/units,si!建立节点n,1,0,0,0n,2,0,1,0!定义质量单元et,1,mass21,r,1,0,1846,0!定义弹簧单元et,2,combin14r,2,10000!建立质量单元type,1real,1e,2!建立弹簧单元type,2real,2e,1,2!约束自由度d,1,alld,2,allddel,2,uyfinish!瞬态动力学求解ANTYPE,transTRNOPT,FULL!阻尼比0.05ALPHAD,0.08976BETAD,0.0274!时间步及间隔t=6000ti=0.005!定义地震波数组*DIM,wavey,ARRAY,t,1,1!导入地震波数据*create,readwave',(e20.8)*end/input,readwave!分步求解time,ti*ikbc,1acel,,wavey(i),nsel,allOUTRES,all,allsolve*enddofinish
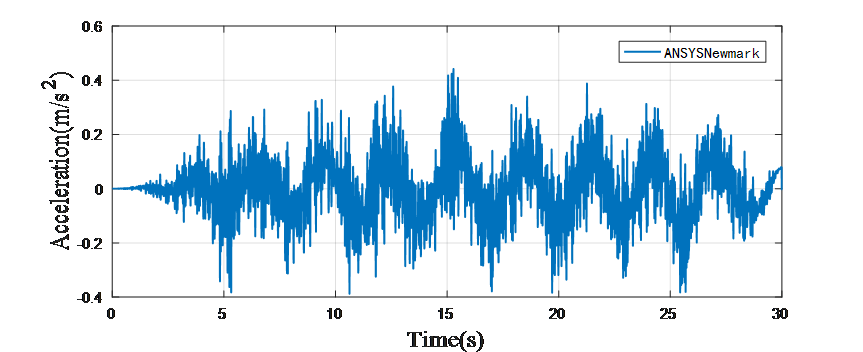
ANSYS加速度时程结果
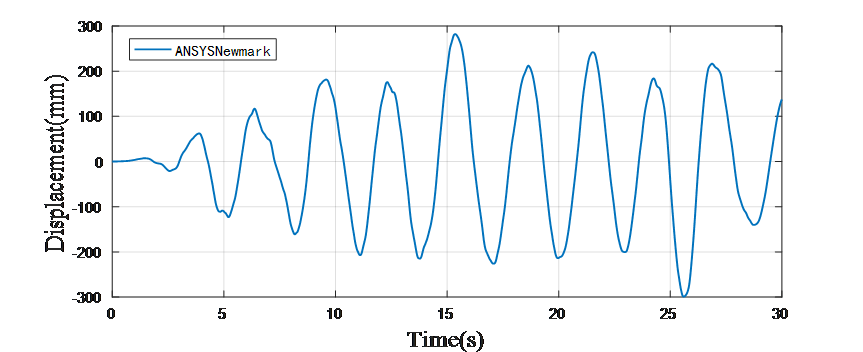
ANSYS位移时程结果
03
OpenSees
Opensees的代码如下:
####### ================ 数据包录入 ====================== ########from openseespy.opensees
import *import numpy as npimport matplotlib.pyplot as plt## =========== 参数 ============ ##def Link(m,damp,k,wave,dt,Amp,g):
wipe()
model('basic', '-ndm', 2, '-ndf', 2)
node(1, 0, 0)
node(2, 0, 1)
mass(2, m, m, 0)
fix(1, 1, 1)uniaxialMaterial('Elastic',1,k)element("twoNodeLink", 1 ,1 ,2 ,'-mat' ,1 ,'-dir', 2)
wavef = np.mat(np.loadtxt(wave)).T #地震波数据读入nwave = len(wavef)
timeSeries('Path', 1, '-filePath', wave, '-dt', dt, '-factor', g)
pattern('UniformExcitation' , 1, 1, '-accel' , 1, '-fact', Amp)system('BandSPD')numberer("RCM")
constraints("Plain")
integrator("LoadControl", 1.0)
test('NormDispIncr', 1.0e-15, 10 )
algorithm("Linear")
#integrator('CentralDifference' )
#algorithm('NewtonLineSearch')
#algorithm('SecantNewton')
integrator('Newmark', 0.5, 0.25 )
#integrator('HHT', 1.0, 0.5, 0.25 )
analysis('Transient')
C1 = 2*damp*(k/m)**0.5
rayleigh(C1, 0, 0, 0)
tFinal = (nwave-1) * dt
tCurrent = getTime()
ok = 0
time = []
Acce = []
Dise = []
Foree = []
while ok == 0 and tCurrent < tFinal:
ok = analyze(1, 0.005)
if ok != 0:
test('NormDispIncr', 1.0e-12, 100, 0)
algorithm('ModifiedNewton', '-initial')
ok =analyze( 1, 0.005)
if ok == 0:
print("ok")
test('NormDispIncr', 1.0e-12, 10 )
algorithm('Newton')
tCurrent = getTime()
time.append(tCurrent)
Acce.append(nodeAccel(2,1))
Dise.append(nodeDisp(2,1))
Foree.append(eleDynamicalForce(1,1))Acc = np.mat([Acce]).T
Acc = Acc + wavef*Amp*g
Dis = np.mat(Dise).T*(-1)
Fore = np.mat(Foree)
return time,Acc,Dis,Fore

OpenSees加速度时程结果
为了方便看清对比,将计算结果以100mm进行相上偏移对比(均以Newmark-β法计算)
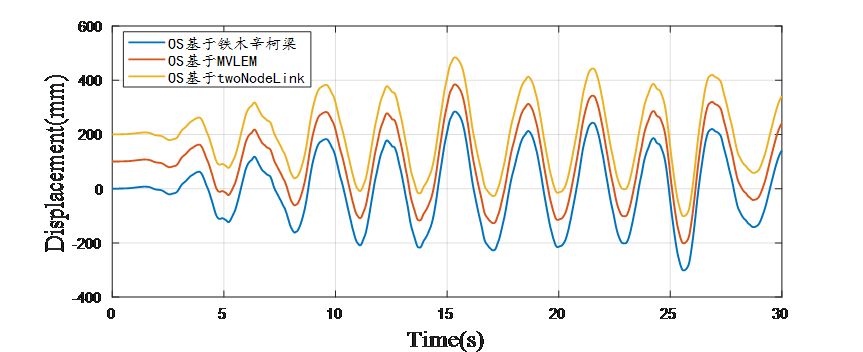
OpenSees位移时程结果
04
Matlab
理论计算均利用专业软件MATLAB完成,计算方法包括分段解析法、杜哈梅积分法、威尔逊-q法、纽马克法。
对比结果:
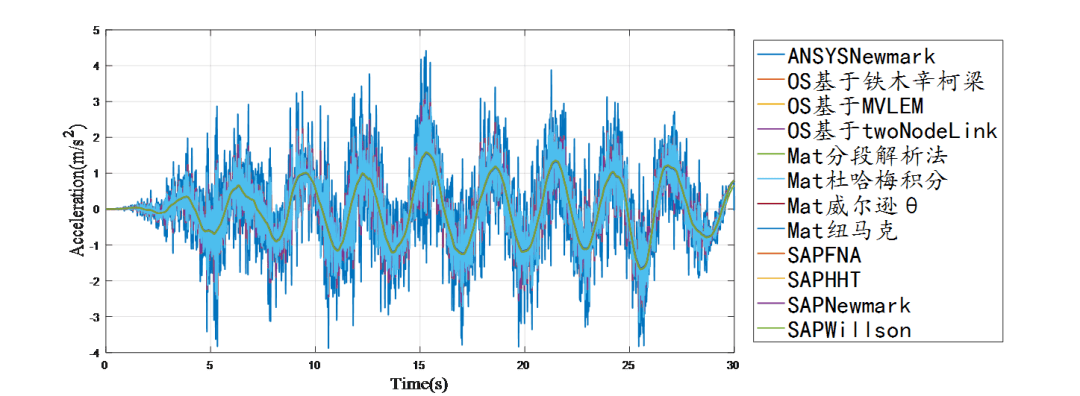
数值软件与理论计算加速度时程对比结果
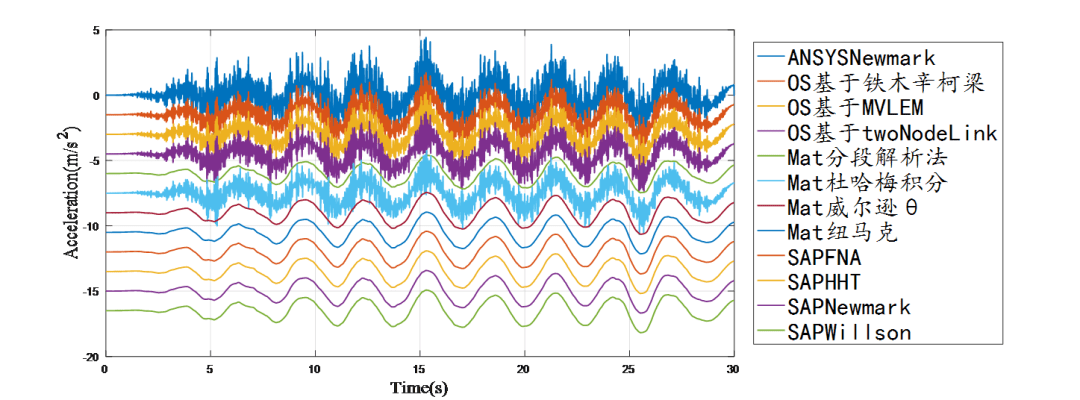
数值软件与理论计算速度时程对比结果
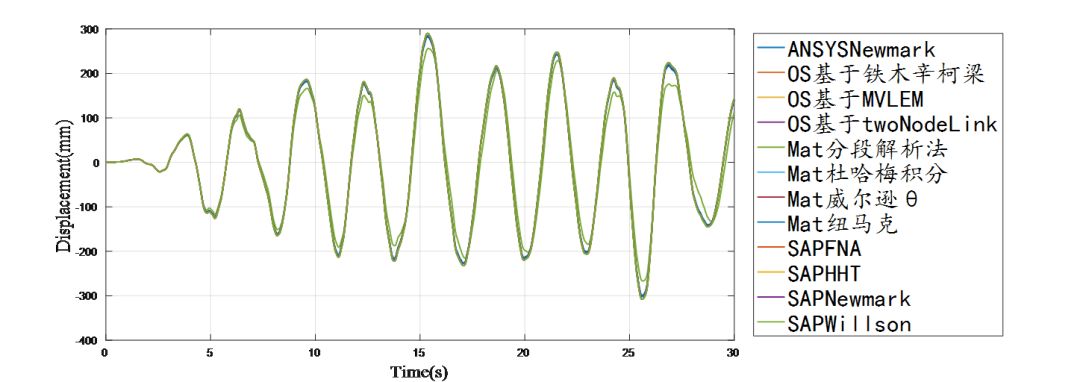
数值软件与理论计算位移时程对比结果
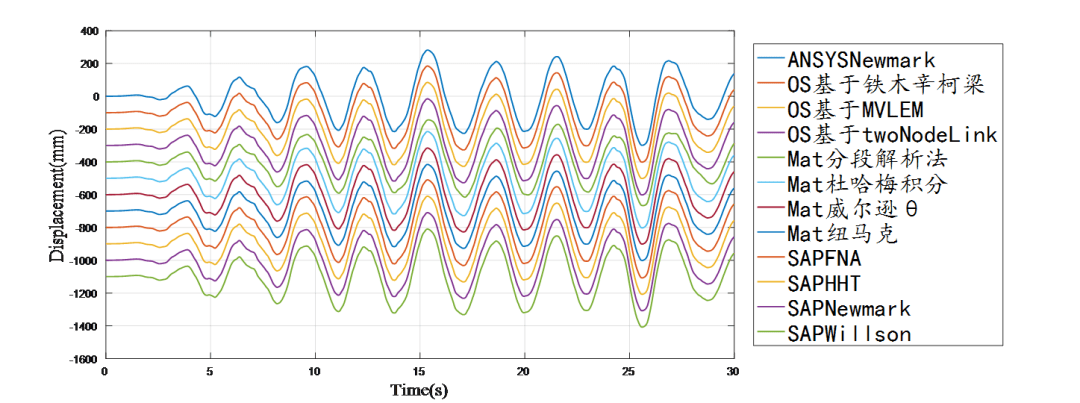
数值软件与理论计算位移时程偏移对比结果
05
结论
各算法下,求解结果高度一致,且误差几乎可以忽略。其中可以发现,加速度/速度/位移在算法中若是通过每一步迭代出来时,即在每个时刻均可通过相应算法得到加速度/速度/位移时,则加速度结果未呈现由于后期求导而产生的背景噪声。若是求解方程的位移结果,则通过位移结果进行求导得到的加速度/速度,会出现较严重的背景噪声(可能由于信号求导产生的高阶误差),且该特性在长周期单质点更为明显。
其中SAP2000为步步算得加速度/速度/位移,而Opensees和ANSYS则采用求导形式,在接下来的文章中会介绍由位移时程获取准确加速度时程的方法,赶紧点个关注吧,这样就不会错过后续的文章啦!

~求关注转赞评~
欢迎关注微信公众号: 建源学堂