简介

    在进行多点输入时程地震反应分析时，为了确定结构的起振时间，必须确定地震波的传播方向，一般多点输入的影响是复杂的，应沿不同的传播方向，根据地震波的传播速度确定各点的相位差，分别计算结构的反应。

    同时应该明确的是，地震地面运动的方向与地震传播的方向是无关的，不能将地震波传播方向与地面运动方向混淆，在同一地震传播方向上，需要考虑不同的地面运动方向的影响。

Step1. 确定各点地震输入时程

    首先应根据工程场地情况确定各点的地震输入时程，通常有以下两种方法：

    场地波动分析方法。考虑土与结构的相互作用，需要根据结构所处场地，建立包括结构和土体的分析模型，在分析模型的边界输入地震波，进行场地波动分析，得到支承各点的地震输入时程。

    相位差简化输入方法。当场地比较均匀，只需要考虑行波效应时，可采用该方法进行分析。利用场地波或以往记录的地震波在结构的基底进行输入，各点输入地震波的形状和峰值大小相同，考虑行波效应后，各点输入的地震波存在一个相位差，这个相位差需要由地震波的传播方向和传播速度共同确定。通常地震波的传播速度范围在100~1000m/s。

    首先根据地震波的传播方向，确定结构的第一个起振点，以此点作为地震波时程的零相位点；假设地震波是沿着传播方向平行传播的，同一波面上的地震波相位相同，根据地震波的传播方向和波速，计算地震波传播到基底各点的时间，确定相应的相位差。

Step2.进行多点输入分析

    建立结构的有限元模型，在基底各点输入前一步得到的地震时程，进行结构的整体分析。根据不同的地震波传播方向，分别确定各点的地震输入时程。同时，因为地震波的振动方向与地震波的传播方向是相互独立的，针对每一个地震波的传播方向，必要时还要考虑地面振动的不同方向，分别进行时程分析。

小结讨论：

    对于桥梁结构，因为下部基础相对独立，基础振动不同步引发的拟静力反应的影响比较明显；而普通建筑结构因为地下室连接在一起，各部分基础的相对变形受到地下室底板的约束，一般不会产生基础的相对变形，拟静力反应的影响比较小。但多点地震输入的另一个影响是因为各点输入的相位不同，相当于输入了一个扭转分量，会产生结构整体的扭转反应，这一点对建筑结构的多点地震分析是主要因素。在考虑了多点地震输入后，对称的多塔楼结构就有可能产生扭转反应，这在单点地震输入分析中是无法实现的。

   建立一个四跨的梁式结构，地震传播到支座之间时间差为5s（此处为了体现多点激励与同步激励差别更明显，选择特别软弱的地基，剪切波速选择非常小），计算分析该结构的动力特性及动力结果。

（注：此结构仅作计算演示，无工程意义）

    为了方便研究利用自主开发的工具将加速度地震输入转化为位移时程输入。

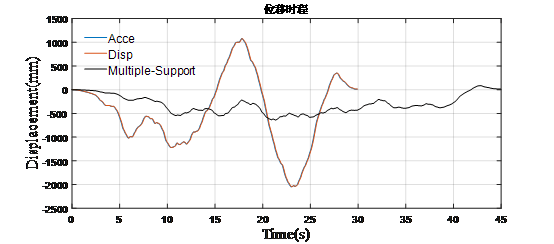
    左图为平常所见的加速度地震波，转换为右图的位移加载时程。为了验证加速度地震波加载和位移时程加载的计算结果是否一致，我们先进行一致激励分析，验证结果。

Step1：计算结构的前三阶周期和前三阶振型

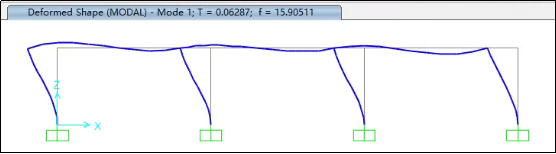
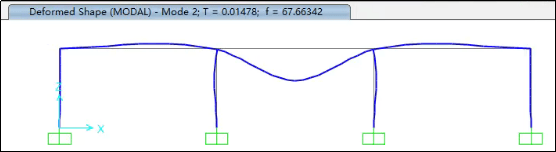
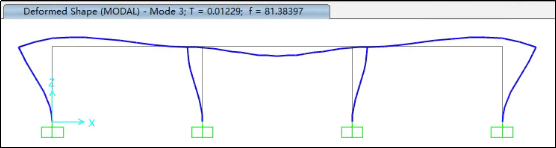
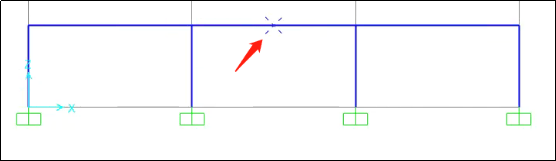
Step2：将加速度时程和位移时程的地震波分别加入结构进行计算分析（均采用直接积分法进行分析），取结构中点(如下图所示)的绝对加速度和绝对位移时程结果进行对比。

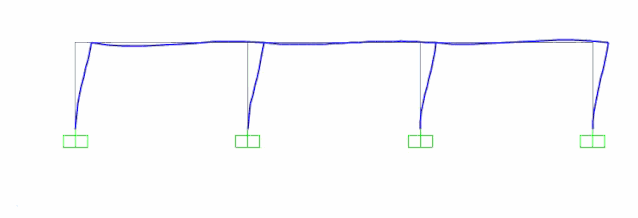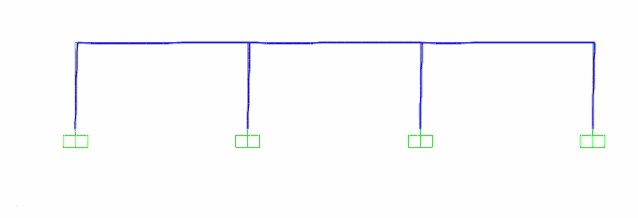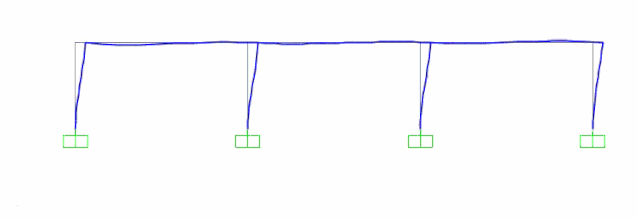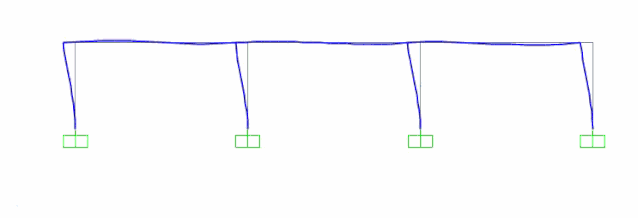
加速度加载结果时程显示

位移加载结果时程显示

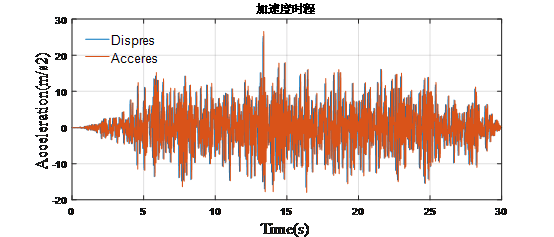
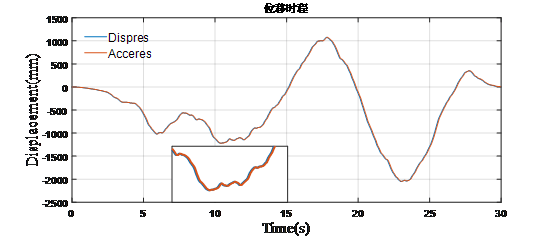
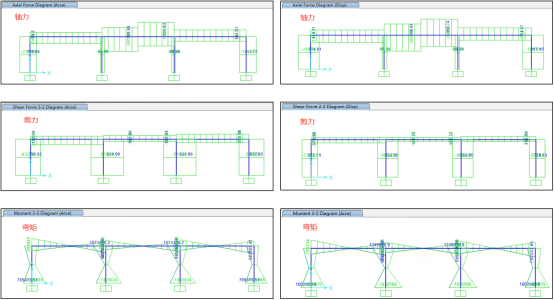
    可见地震波通过加速度加载和位移加载结果基本一致，验证了做法有效性和可实施性，内力对比如下图所示，也呈现基本一致，说明加载方法可行。

Step3：考虑行波效应的多点激励施加，施加方式如下图所示，且依旧提结构中点的绝对位移时程进行对比。

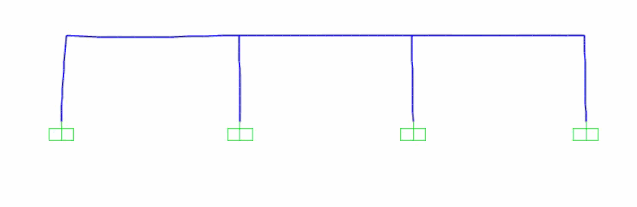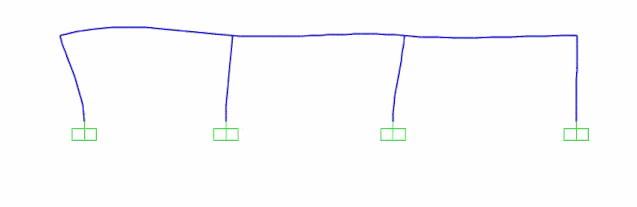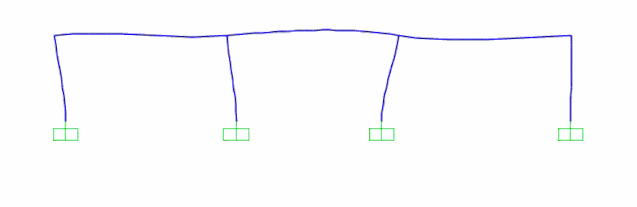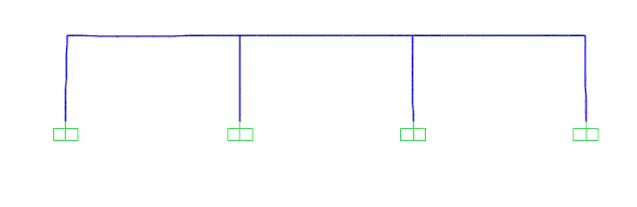
多点激励加载结果时程显示

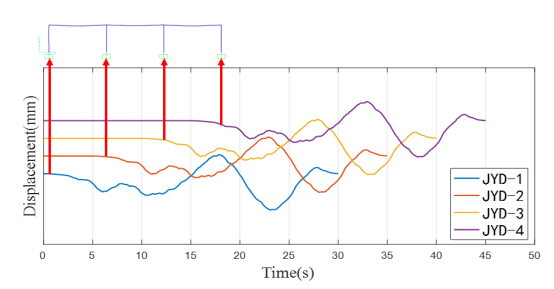
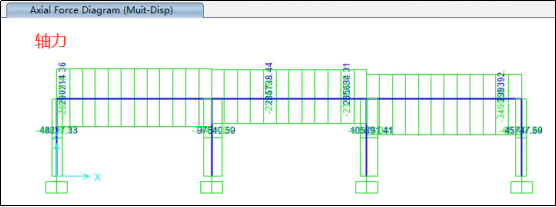
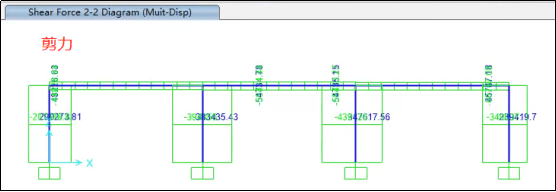
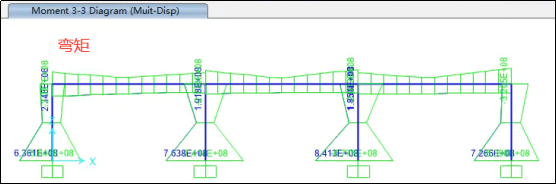
    可以发现，通过多点激励之后，结构的内力在各个支座不协同运动下增大了许多，而由于结构支座不协同运动，导致中点的位移反而偏小。

    接下来将原理阐述下，感兴趣的看官可以继续一起探讨。

    首先谈谈支座静位移时的动力方程，将结构自由度分为两类，即为内部自由度和支座自由度，于是平衡方程的分块矩阵为：

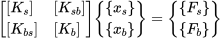
     由于我们采用的是位移加载模式，因此一般支座位位移量，外荷载为已知，而结构内部自由度位移和反力为未知量为未知量，将上式展开可得：

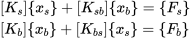
     上面第一个式子又可写成：

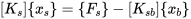
    若无外荷载激励而仅产生支座位移，可变形为：

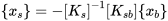
    这个就是支撑节点发生位移时在非支撑节点产生的静位移。

    考虑多点激励时，动力方程为：

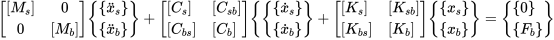
    在结构承受随时间变化的支座移动时，结构的反应来源由两部分：支座移动引起的结构反应，称为拟静力反应；支座移动加速度导致的惯性力引起的结构反应，称为动力反应，因此将位移表示为：

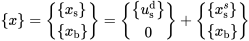
    由前半部分得到的可知：

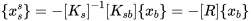
    且求一二阶倒数：

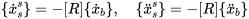
    将上式子带入动力方程可得：

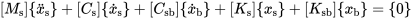
    若阻尼力相对惯性力而言可忽略不计，则式子可变形为：

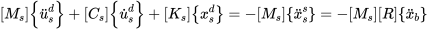
    上面的推导就是多点激励的动力平衡方程。由推导可以看出拟静力反应和动力反应均与结构刚度有关，对于线性结构，拟静力反应和动力反应可以分别单独求解。

概念为先，机理为本，下期见！

建源之光——工程侠