写在前文

    壳结构作为一类典型的薄壁构件，在航空航天、土木工程、机械制造等领域具有广泛应用。其核心特征表现为沿厚度方向的尺寸远小于另外两个方向，这一几何特性使得基于三维连续体理论的直接分析面临计算效率与精度的权衡难题。 

    壳单元通过将三维问题简化为中面二维分析，在保留关键力学行为描述能力的同时显著降低计算成本，成为解决此类问题的核心数值工具。本文系统梳理壳单元的理论基础、分类体系、选型策略及应用要点，为工程仿真中壳单元的合理选用提供理论支撑与实践指导。

 【相关阅读】

【JY】板壳单元的分析详解

1 壳单元理论基础与分类

1.1 壳单元基本假设

    壳单元基于以下基本假设：平面截面垂直于壳中面且在变形过程中保持平面（Kirchhoff-Love 假设）。这一假设认为，垂直于壳面的横截面在变形过程中保持为平面，并且在变形后仍然垂直于壳的中面。Abaqus 壳单元正是基于这一理论基础，将三维问题简化为二维分析，从而提高计算效率。

   需要注意的是，Abaqus 壳单元并不要求壳的厚度必须小于其平面尺寸的 1/10。在高度细化的网格中，壳单元的厚度可能大于其平面尺寸，但这种情况并不推荐，此时连续体单元（实体单元）可能更适合。

1.2 壳单元分类与特性

Abaqus 提供了多种壳单元类型，主要分为以下几类：

1. 一般壳单元：如 S4R、S3R、SAX1、SAX2、SAX2T 等，对于薄壳和厚壳问题的应用均有效，且考虑了有限薄膜应变。

2. 薄壳单元：如 STRI3、STRI35、STRI65、S4R5、S8R5、S9R5、SAXA 等，强化了基尔霍夫条件，即垂直于壳中截面的平面保持垂直于中截面。

   

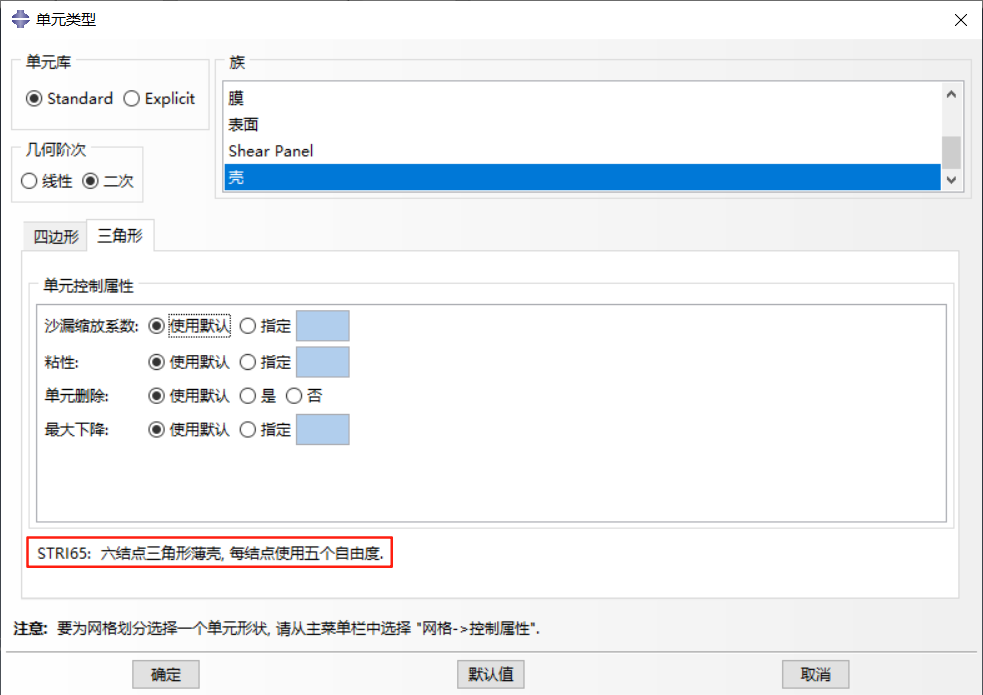
3. 厚壳单元：如 S8R、S8RT 等，二阶四边形单元，在小应变和载荷使计算结果沿壳的跨度方向上平缓变化的情况下，比普通单元产生的结果更精确。

   

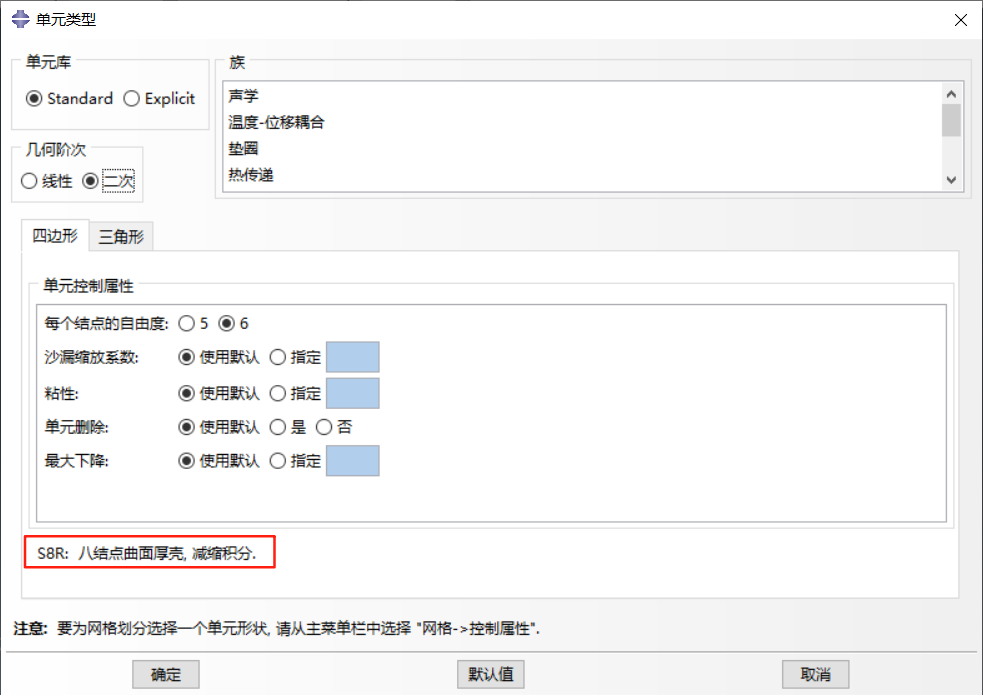
4. 连续壳单元：如 SC6R（6 节点线性单元）和 SC8R（8 节点缩减积分单元），用于复合材料层合板建模，能够更准确地描述复合材料厚度方向的剪切变形。

   

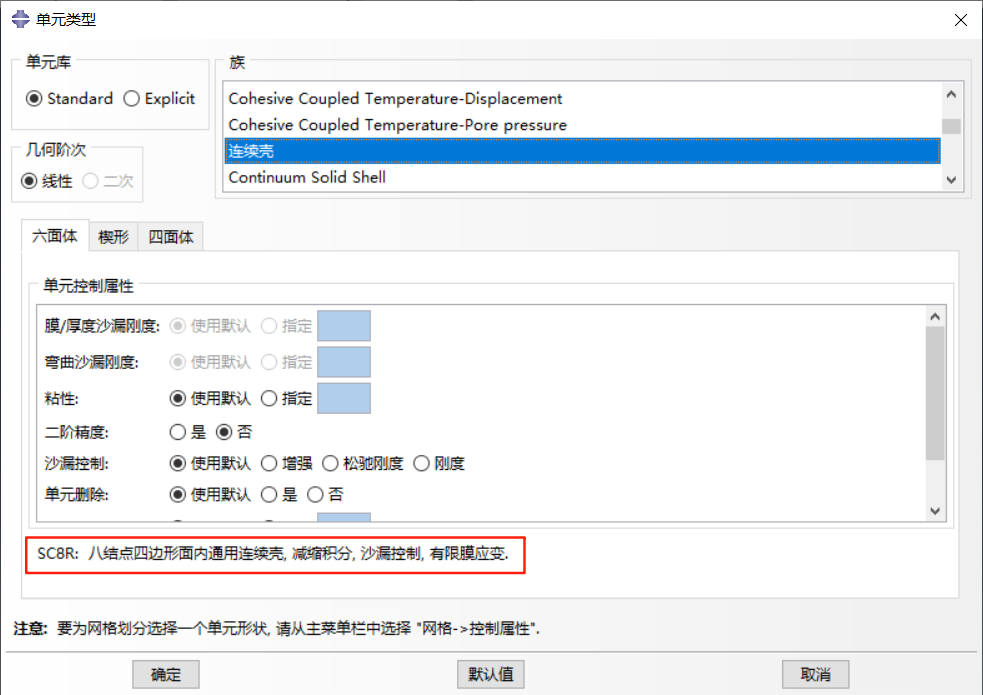
1.3 壳单元自由度与坐标系统

    壳单元的自由度包括三个平动自由度（沿三个坐标轴方向的位移）和三个转动自由度（绕三个坐标轴的旋转）。壳单元法线方向决定了单元的正和负表面，为了正确地定义接触和解释输出数据，必须清楚其对应的是哪个面。壳法线还定义了施加在单元上正压力载荷的方向，并可以在 Abaqus/Post 中显示。

    壳单元利用材料方向局部化到每个单元。在大位移分析中，局部材料轴随单元而转动。ORIENTATION 被用来定义非默认的局部坐标系统。单元的变量，如应力和应变，在局部方向输出。而TRANSFORM 定义节点的局部坐标系，集中载荷和边界条件被应用在局部坐标系中。所用节点的输出，如位移，也默认为基于局部的坐标系。

2 壳单元选择策略与应用场景

2.1 壳单元与实体单元的选择比较

在决定使用壳单元还是实体单元时，应考虑以下因素：

1. 结构几何特征：壳单元适用于模拟有一维尺寸（厚度）远小于另外两维尺寸，且垂直于厚度方向的应力可以忽略的结构。如果结构的厚度与其他尺寸相比并不显著较小，或者需要考虑厚度方向的应力分布，则应考虑使用实体单元。

2. 分析目标：如果分析目标是结构的整体变形、应力分布及屈曲特性，壳单元通常足够。如果需要精确模拟厚度方向的应力分布或层间应力，则应使用实体单元或连续壳单元。

3. 计算效率：壳单元由于将三维问题简化为二维分析，计算效率通常高于实体单元，特别是对于大型复杂模型。然而，对于某些复杂问题，如高度非线性或接触问题，壳单元可能需要更精细的网格才能达到与实体单元相当的精度。

4. 材料特性：对于复合材料层合板，Abaqus 提供了常规壳、连续壳和连续实体三种建模方法。常规壳方法适用于薄壳结构，连续壳方法适用于中等厚度结构并能更好地模拟层间剪切变形，而连续实体方法则适用于无法忽略法向应力或需要求解精确层间应力的情况。

2.2 不同壳单元类型的选择策略

针对不同的工程应用，壳单元的选择策略如下：

1. 一般壳单元：线性、有限薄膜应变、四边形壳单元（S4R）是较完备的而且适合于普通范围的应用；线性、有限薄膜应变、三角形壳单元（S3R）可作为通用的壳单元来应用。由于在单元内部近似为应变场，精细的网格划分可用于求解弯曲变形和高应变梯度。

2. 薄壳单元：对于一般的小变形薄壳，四边形或三角形的二次壳单元是很有效的。它们对剪力自锁和薄膜锁死不敏感。在接触模拟中不应选用二阶三角形壳单元（STRI65），而应采用 9 节点的四边形壳单元（S9R5）。

3. 厚壳单元：考虑到在复合材料层合壳模型中剪切柔度的影响，应采用 "厚" 壳单元（S4R、S3R、S8R 等）。对于单一材料制造的各向同性壳体，如果厚度和跨度之比在 1/20－1/10 之间，认为是厚壳问题；如果比值小于 1/30，则认为是薄壳问题；若介于 1/30－1/20 之间，则介于二者均可进行有效的计算。

4. 连续壳单元：连续壳建模方法与常规壳相比，能够更准确地描述复合材料厚度方向的剪切变形，同时仍保持较高的计算效率。该方法本质上是一种三维单元模型，但其几何形状和计算逻辑接近传统的壳单元，适用于中等厚度的复合材料建模。

2.3 复合材料层合壳的特殊考虑

对于复合材料层合壳，Abaqus 提供了专门的建模方法和单元类型：

1. 常规壳方法：常规壳复合材料的建模过程使用 "复合材料铺层 (Composite Layup)" 工具创建。该方法基于经典壳理论，将复合材料层合板建模为一系列薄层，同时忽略厚度方向的复杂剪切变形。该方法使用二维壳单元进行离散化，常用的单元包括 S4、S4R、S8R 等。

2. 连续壳方法：连续壳建模方法使用三维网格离散化，使用连续壳单元，包括 SC6R（6 节点线性单元）、 SC8R（8 节点缩减积分单元）或者CSS8（8节点单元）。连续壳方法能够更准确地描述复合材料厚度方向的剪切变形，同时仍保持较高的计算效率，适用于中等厚度的复合材料建模。

   

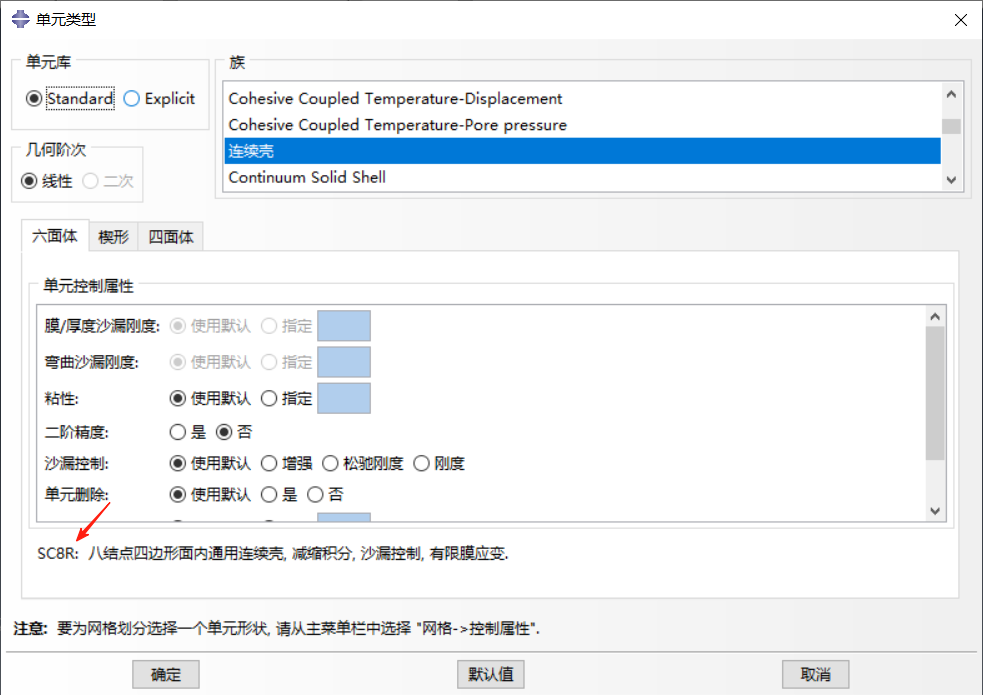
3. 连续实体方法：连续实体建模方法完全基于三维实体单元，将每一层复合材料建模为一个独立的实体层。它可以全面捕捉复合材料厚度方向的应力分布与剪切变形，是最精确的建模方法，适用于厚的复合材料结构的精确分析。

3 各类壳单元详解与应用

3.1 线性壳单元（如 S4R、S3R）

理论基础：线性壳单元基于线性插值函数，节点仅位于单元的顶点，各方向采用线性插值。它们考虑了有限薄膜应变，能够处理大位移和中等旋转问题，但无法精确模拟复杂的非线性变形。

适用场景：线性壳单元适用于各种薄壳和厚壳结构，特别是当结构变形相对简单且对精度要求不是极高的情况。S4R 是最常用的壳单元类型，具有良好的稳定性和广泛的适用性，适用于大多数工程应用。

优缺点分析：

• 优点：计算效率高；对各种几何形状的适应性强；能够处理大位移和中等旋转；在大多数情况下提供足够的精度。

• 缺点：对复杂变形和应力集中区域的模拟精度有限；在某些情况下可能出现剪切自锁或薄膜自锁；对于高精度分析或复杂非线性问题，可能需要更精细的网格或更高阶的单元。

使用注意事项：

• 对于以弯曲为主的结构，应确保沿厚度方向有足够的单元数量，通常至少 2-3 个积分点，以捕捉厚度方向的应力梯度。

• 在接触分析中，线性壳单元通常比二次单元更稳定，收敛性更好。

• 对于复合材料层合壳，线性壳单元（如 S4R）可用于常规壳建模方法，但可能需要通过定义复合材料铺层来准确模拟层合板特性。

• 在需要高精度结果的区域，如应力集中处或几何突变处，应考虑使用二次壳单元或进行局部网格细化。

3.2 二次壳单元（如 S8R、S9R5）

理论基础：二次壳单元基于二次插值函数，在每条边上有中间节点，能够更精确地模拟复杂变形和应力分布。二次壳单元通常采用缩减积分技术，以提高计算效率并避免剪切自锁问。

适用场景：二次壳单元适用于对精度要求高、变形复杂的薄壳结构，特别是存在应力集中或需要精确模拟曲面变形的情况。它们对剪力自锁和薄膜锁死不敏感，适用于各种载荷条件下的薄壳结构响应分析。

优缺点分析：

• 优点：能够更精确地模拟复杂变形和应力分布；对剪力自锁和薄膜锁死不敏感；在小变形情况下提供极高的精度；适用于各种薄壳结构。

• 缺点：计算成本高于线性壳单元；在大变形或接触问题中可能需要更精细的网格；对于某些复杂非线性问题，收敛性可能不如线性单元。

使用注意事项：

• 在接触模拟中不应选用二阶三角形壳单元（STRI65），而应采用 9 节点的四边形壳单元（S9R5），后者在接触分析中表现更好。

• 二次壳单元对网格质量更为敏感，应避免使用过度扭曲或不规则的单元。

• 对于复合材料层合壳的小变形分析，二次壳单元（如 S9R5）可提供极高的精度，但需要正确定义复合材料铺层和材料方向。

• 在使用二次壳单元时，应注意单元的积分点位置，应力和其他结果通常在积分点处计算，然后外推到节点，可能会导致节点处的结果存在一定误差。

3.3 连续壳单元（SC6R、SC8R）

理论基础：连续壳单元是一种三维单元模型，但其几何形状和计算逻辑接近传统的壳单元。它使用三维网格离散化，但通过特殊的公式将三维问题简化为二维分析，从而在保持壳单元效率的同时，能够更准确地描述厚度方向的剪切变形。

适用场景：连续壳单元适用于中等厚度的复合材料层合板，特别是需要考虑层间剪切变形的情况。它们能够更准确地描述复合材料厚度方向的剪切变形，同时仍保持较高的计算效率，适用于中等厚度结构的高精度分析。

优缺点分析：

• 优点：能够更准确地模拟厚度方向的剪切变形；适用于中等厚度结构；在保持壳单元效率的同时提供更高的精度；能够处理复合材料层合板的复杂行为。

• 缺点：不能应用于超弹性和泡沫材料模型；对于非常薄的壳，连续壳单元收敛性可能较差；在 Abaqus/Explicit 中，连续壳单元的厚度方向尺寸（尺寸较小）将影响稳定时间增量。

使用注意事项：

• 连续壳单元主要用于复合材料层合板的建模，特别是需要考虑层间剪切变形的中等厚度结构。

• 在 Abaqus/CAE 中，连续壳单元需要通过 "Composite Layup" 工具创建，并正确定义铺层顺序和材料方向。

• 对于连续壳单元，应确保沿厚度方向有足够的积分点（通常等于铺层数），以准确捕捉各层的应力分布。

• 在 Abaqus/Explicit 中使用连续壳单元时，应注意单元尺寸对稳定时间增量的影响，可能需要更精细的时间步长控制。

• 连续壳单元不适用于需要考虑厚度方向法向应力的情况，此时应使用连续实体方法。

3.4 特殊壳单元类型

Abaqus 还提供了一些特殊类型的壳单元，适用于特定的应用场景：

1. 轴对称壳单元：如 SAX1、SAX2、SAX2T 等，用于模拟轴对称壳结构，如圆柱壳、圆锥壳等。这些单元能够显著减少模型规模，提高计算效率，特别适用于具有轴对称几何和载荷的问题。

2. 薄壳单元：如 S4R5、S8R5 等，强化了基尔霍夫条件，适用于非常薄的壳结构。这些单元假设垂直于壳中面的平面在变形后保持垂直，忽略了横向剪切变形，适用于厚度与其他尺寸之比小于 1/30 的薄壳。

3. 厚壳单元：如 S8R、S8RT 等，考虑了横向剪切变形，适用于厚度与其他尺寸之比在 1/20 至 1/10 之间的厚壳结构。这些单元能够更准确地模拟厚壳的剪切变形和应力分布。

4. 可扩展壳单元：如 S6、S9 等，允许用户定义自定义的壳截面形状和材料分布，适用于特殊截面或非均质材料的壳结构。

使用注意事项：

• 轴对称壳单元仅适用于几何形状和载荷均轴对称的问题，否则会导致严重的计算误差。

• 薄壳单元和厚壳单元的选择应基于结构的厚跨比，通常厚跨比小于 1/30 时使用薄壳单元，介于 1/30 和 1/10 之间时使用一般壳单元，大于 1/10 时考虑使用厚壳单元或实体单元。

• 对于复合材料层合板，特殊壳单元（如连续壳单元）通常比普通壳单元更合适，因为它们能够更好地模拟层间剪切变形和各向异性材料特性。

• 在使用任何特殊壳单元之前，应充分了解其理论基础和适用范围，确保其适合特定的工程问题。

4 壳单元使用注意事项

4.1 壳单元方向与截面定义

1. 壳单元法线方向：壳单元法线方向决定了单元的正和负表面，为了正确地定义接触和解释输出数据，必须知道其对应的是哪个面。壳法线还定义了施加在单元上正压力载荷的方向，并可以在 Abaqus/Post 中显示。在创建壳单元时，应注意法线方向是否正确，否则可能导致接触定义错误或载荷方向相反。

2. 壳截面定义：壳单元的横截面特性可以由沿厚度方向的数值积分确定（*SHELL SECTION），或在分析开始时应用计算的横截面刚度（*SHELL GENERAL SECTION）。*SHELL GENERAL SECTION 非常有效，但仅用于线性材料，而SHELL SECTION 可用于线性和非线性材料。数值积分在沿壳厚度方向的一系列积分点上进行，这些积分点就是单元变量可以被输出的位置。最外层的积分点位于壳单元的表面。

3. 复合材料铺层定义：对于复合材料层合壳，壳截面定义变得更加复杂，需要定义各铺层的材料、厚度、方向和顺序。在 Abaqus/CAE 中，可以通过 "Composite Layup" 工具方便地定义复合材料铺层。常规壳方法将层合板建模为一系列薄层，同时忽略厚度方向的复杂剪切变形；连续壳方法则使用三维网格离散化，能够更准确地描述厚度方向的剪切变形。

4.2 壳单元网格划分最佳实践

1. 网格密度控制：壳单元的网格密度应根据结构的几何特征、载荷条件和分析目标确定。在应力集中区域、几何突变处或载荷复杂的区域，应使用更精细的网格。对于以弯曲为主的结构，沿厚度方向应至少划分 2-3 个单元，以捕捉厚度方向的应力梯度。对于高精度分析，可能需要更多的单元。

2. 单元形状优化：壳单元应尽量保持规则的形状，如接近正方形的四边形单元。应避免使用高度扭曲或长宽比过大的单元，这些单元可能导致计算精度下降或收敛困难。对于三角形单元，应尽量使其接近等边三角形，避免出现尖锐角度。

3. 混合单元类型的使用：在同一模型中可以混合使用四边形和三角形单元，但应注意避免在关键区域使用三角形单元，因为它们通常精度较低。在几何复杂区域，可以使用三角形单元过渡，但应尽量限制其使用范围。

4. 结构化网格的优势：对于规则几何区域，应优先使用结构化网格划分技术，生成高质量的四边形网格。结构化网格不仅质量高，而且计算效率更高，能够提供更准确的结果。在可能的情况下，应避免使用自由网格划分，特别是对于高精度分析。

4.3 壳单元结果评估与解释

1. 应力结果位置：壳单元的应力结果通常在壳的顶面、中面和底面的积分点处计算，然后外推到节点。在解释结果时，应注意结果是来自积分点还是节点，积分点结果通常更准确，但节点结果更便于显示和比较。

2. 层间应力评估：对于复合材料层合壳，层间应力（特别是层间剪切应力）是评估结构性能的重要指标。常规壳单元由于忽略了厚度方向的剪切变形，可能无法准确预测层间应力。在这种情况下，应使用连续壳单元或连续实体方法，以获得更准确的层间应力结果。

3. 薄膜应力与弯曲应力的区分：壳单元结果通常可以分解为薄膜应力（平面内应力）和弯曲应力（厚度方向应力）。在评估结构性能时，应分别考虑这两种应力分量，特别是对于薄壁结构，弯曲应力可能占主导地位。

4. 结果验证方法：为确保壳单元分析结果的准确性，应进行网格敏感性分析和结果验证。可以通过比较不同网格密度下的结果、与解析解或实验数据对比，或使用更精确的实体单元模型进行验证。对于高精度分析，这些验证步骤尤为重要。